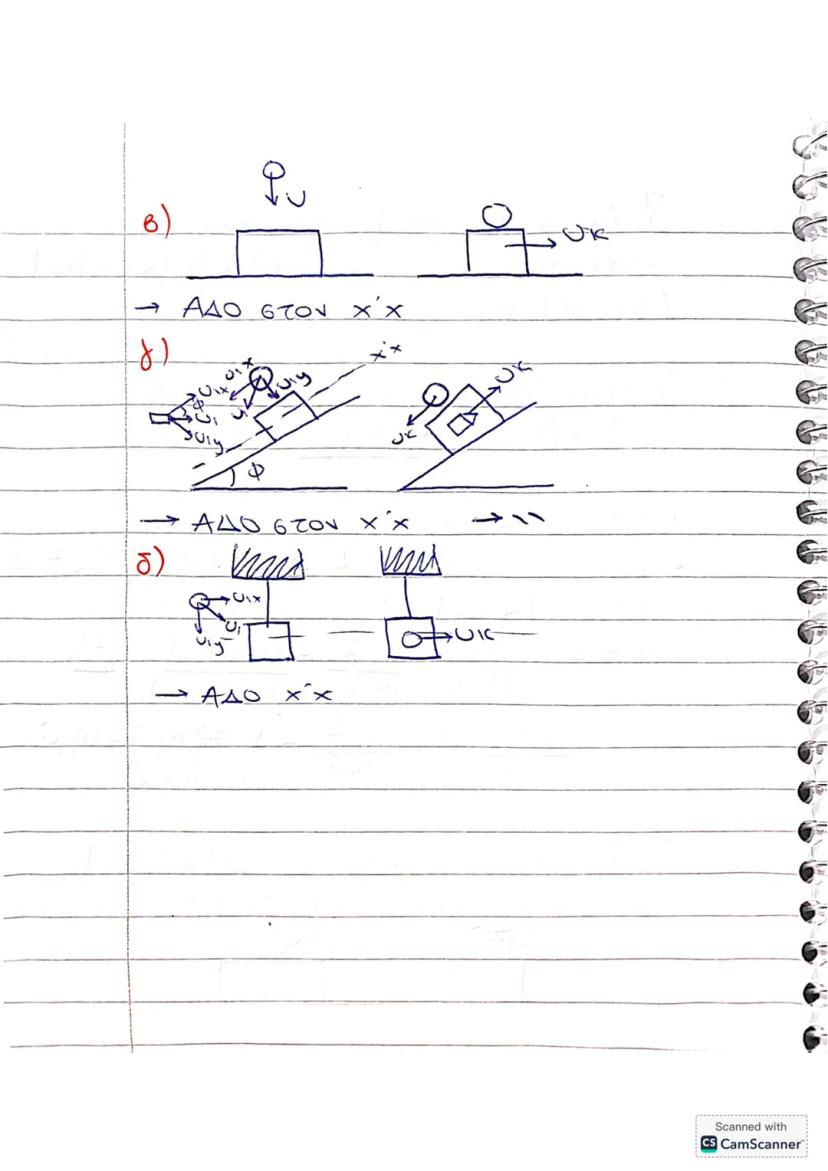
Οι κρούσεις είναι ένα από τα πιο σημαντικά κεφάλαια της... Δες περισσότερα
Κάνε εγγραφή για να δεις το ΠΕΡΙΕΧΟΜΕΝΟΕίναι δωρεάν!
Πρόσβαση σε όλα τα έγγραφα
Βελτίωσε τους βαθμούς σου
Γίνε μέλος με εκατομμύρια μαθητές
Κάνοντας εγγραφή αποδέχεσαι τους Όρους Χρήσης και την Πολιτική Απορρήτου