Οι Τρεις Κβαντικοί Αριθμοί
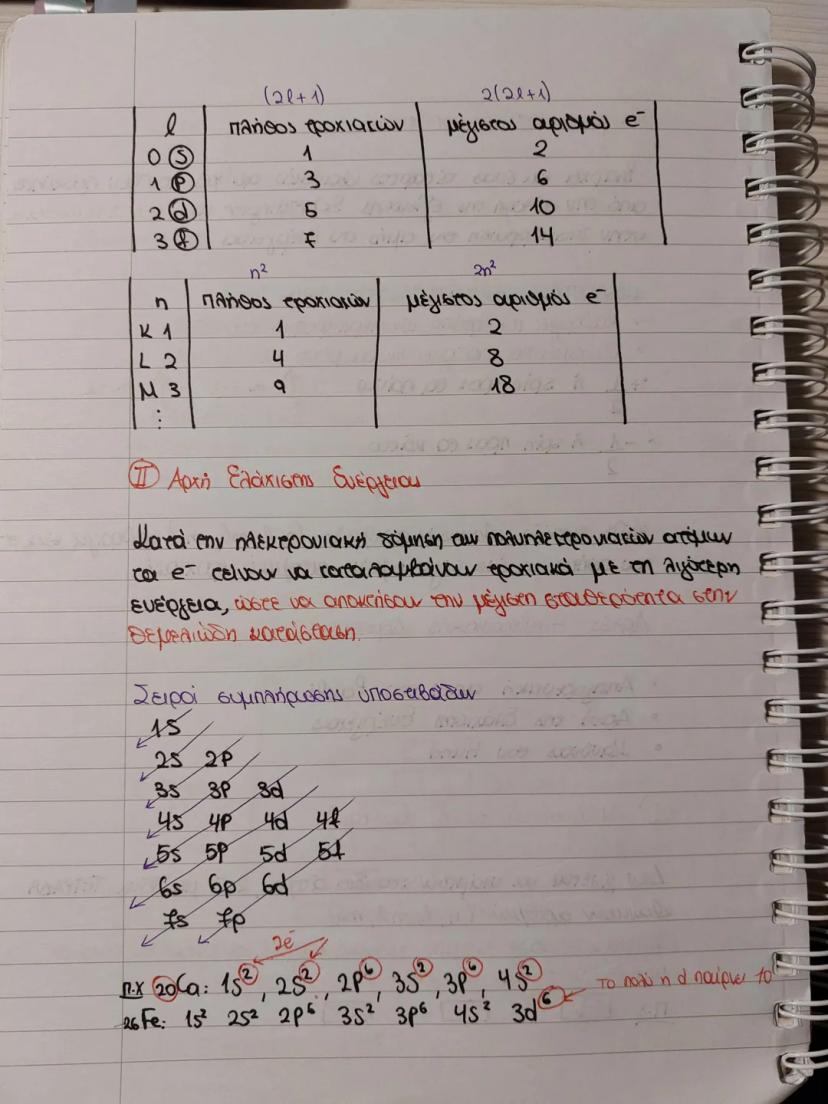
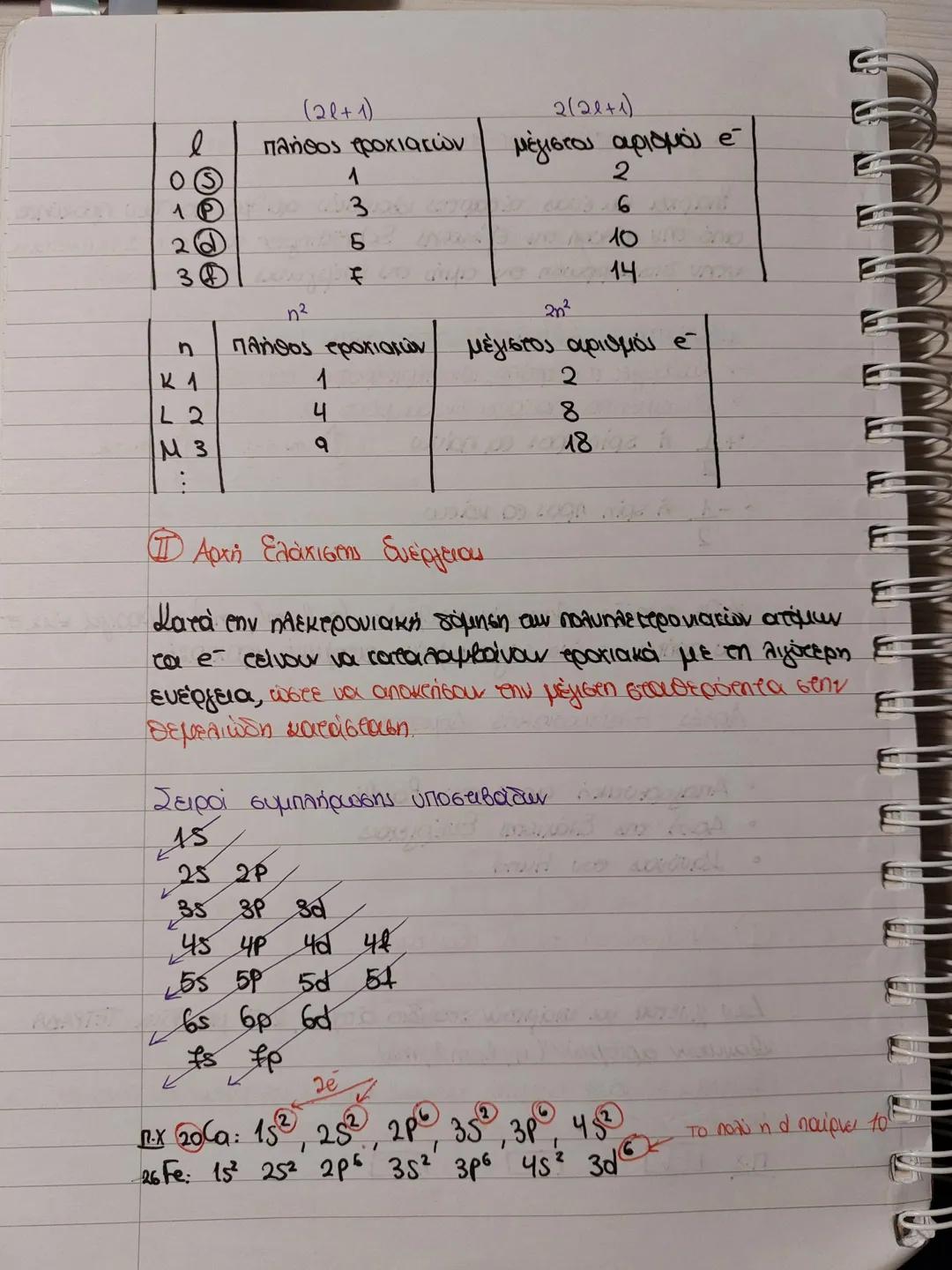
Ο κύριος κβαντικός αριθμός (n) παίρνει θετικές ακέραιες τιμές (1,2,3...) και καθορίζει το μέγεθος του ηλεκτρονιακού νέφους καθώς και την ενέργεια. Όσο μεγαλύτερο το n, τόσο μεγαλύτερη η απόσταση από τον πυρήνα.
Ο δευτερεύων κβαντικός αριθμός (l) παίρνει τιμές 0,1,2...n-1 και καθορίζει το σχήμα του ηλεκτρονιακού νέφους. Κάθε τιμή αντιστοιχεί σε διαφορετικό τροχιακό: l=0 (s), l=1 (p), l=2 (d), l=3 (f).
Ο μαγνητικός κβαντικός αριθμός (ml) παίρνει τιμές από -l έως +l και καθορίζει τον προσανατολισμό του τροχιακού στο χώρο. Για παράδειγμα, αν l=1, τότε ml=-1,0,+1 (3 τροχιακά p).
Χρήσιμο: Στα πολυηλεκτρονιακά άτομα, η ενέργεια εξαρτάται από το άθροισμα n+l.