Θεωρία του Bohr και Κβαντισμός

Η θεωρία του Bohr επανάστασε τον τρόπο που βλέπουμε τα άτομα. Σύμφωνα με την 1η συνθήκη του, τα ηλεκτρόνια δεν κινούνται όπου θέλουν, αλλά μόνο σε συγκεκριμένες τροχιές με καθορισμένη ενέργεια.

Το μυστικό είναι ότι η ενέργεια είναι κβαντισμένη - δηλαδή παίρνει μόνο συγκεκριμένες τιμές, όπως τα χρήματα που μπορείς να έχεις μόνο σε πολλαπλάσια των 5 λεπτών. Η ενέργεια ενός ηλεκτρονίου δίνεται από τον τύπο E = -2,18·10⁻¹⁸/n² J.

Το αρνητικό πρόσημο σημαίνει ότι πρέπει να δώσεις ενέργεια για να "κλέψεις" ένα ηλεκτρόνιο από το άτομο. Όταν ένα ηλεκτρόνιο απορροφά ενέργεια, πηγαίνει σε υψηλότερη στιβάδα (διεγερμένη κατάσταση), αλλά γρήγορα επιστρέφει εκπέμποντας φωτόνια με συγκεκριμένη ενέργεια.

💡 Θυμήσου: Στη θεμελιώδη κατάσταση, όλα τα ηλεκτρόνια βρίσκονται όσο πιο κοντά στον πυρήνα γίνεται - εκεί έχουν τη μικρότερη ενέργεια!

Μεταπτώσεις και Φάσματα

Όταν ένα ηλεκτρόνιο "πέφτει" από υψηλότερη σε χαμηλότερη στιβάδα, εκπέμπει φωτόνιο με ενέργεια ΔΕ = Eτελική - Eαρχική. Αυτή η ενέργεια μετατρέπεται σε φως με συχνότητα f = ΔΕ/h, όπου h είναι η σταθερά του Planck (6,63·10⁻³⁴ J·s).

Για παράδειγμα, στη μετάπτωση από n=4 σε n=1, το ηλεκτρόνιο εκπέμπει περισσότερη ενέργεια από ό,τι στη μετάπτωση n=3 σε n=2. Αυτό σημαίνει ότι το πρώτο φωτόνιο έχει μικρότερο μήκος κύματος (λ₁ < λ₂).

Όταν θερμαίνουμε μια αέρια ουσία, παράγεται γραμμικό φάσμα με συγκεκριμένες γραμμές. Αντίθετα, οι στερεές και υγρές ουσίες δίνουν συνεχές φάσμα. Κάθε στοιχείο έχει το δικό του μοναδικό φάσμα - σαν δακτυλικό αποτύπωμα!

💡 Προσοχή: Για να διεγερθούν όλα τα άτομα σε ένα δείγμα, χρειάζονται τόσα φωτόνια όσα και τα άτομα (χρησιμοποίησε τον αριθμό Avogadro)!

Από τον Bohr στη Σύγχρονη Κβαντομηχανική

Η θεωρία του Bohr λειτουργούσε μόνο για μονοηλεκτρονιακά άτομα (H, He⁺, Li²⁺) και δεν εξηγούσε τα πολυηλεκτρονιακά άτομα. Έτσι, οι επιστήμονες ανέπτυξαν νέες θεωρίες που άλλαξαν τελείως την εικόνα μας για τα άτομα.

Ο De Broglie πρότεινε ότι τα μικρά σωματίδια έχουν διττή φύση - είναι και σωματίδια και κύματα. Ένα ηλεκτρόνιο που κινείται γρήγορα συμπεριφέρεται σαν κύμα με μήκος κύματος λ = h/mv.

Ο Heisenberg διατύπωσε την αρχή της αβεβαιότητας: δεν μπορούμε να γνωρίζουμε ταυτόχρονα με ακρίβεια τη θέση και την ταχύτητα ενός ηλεκτρονίου. Αυτό δεν είναι τεχνικό πρόβλημα - είναι θεμελιώδης νόμος της φύσης!

Όλες αυτές οι ιδέες οδήγησαν στην εξίσωση του Schrödinger και στην έννοια των ατομικών τροχιακών - χώρων όπου έχουμε πιθανότητα να βρούμε ένα ηλεκτρόνιο.

💡 Βασική διαφορά: Δεν μιλάμε πλέον για συγκεκριμένες τροχιές, αλλά για περιοχές πιθανότητας!

Ατομικά Τροχιακά - Οι "Κατοικίες" των Ηλεκτρονίων

Τα ατομικά τροχιακά είναι οι τρισδιάστατοι χώροι όπου έχουμε 99% πιθανότητα να βρούμε ένα ηλεκτρόνιο. Κάθε τροχιακό έχει τρία χαρακτηριστικά: μέγεθος, σχήμα και προσανατολισμό στο χώρο.

Μπορούμε να παραστήσουμε τα τροχιακά με τρεις τρόπους: με στίγματα (όσο πιο πυκνά, τόσο μεγαλύτερη η πιθανότητα), με καμπύλες που περικλείουν το 99% της πιθανότητας, ή με γραφικές παραστάσεις που δείχνουν πώς αλλάζει η πιθανότητα με την απόσταση από τον πυρήνα.

Η κυματοσυνάρτηση ψ από μόνη της δεν έχει φυσικό νόημα, αλλά το ψ² μας δίνει την πιθανότητα εύρεσης του ηλεκτρονίου σε κάθε σημείο. Αυτή είναι η βάση για να κατανοήσουμε τη δομή των ατόμων!

💡 Σημαντικό: Το τροχιακό δεν είναι η διαδρομή του ηλεκτρονίου, αλλά ο χώρος όπου πιθανότατα θα το βρούμε!

Κβαντικοί Αριθμοί - Η "Διεύθυνση" κάθε Ηλεκτρονίου

Κάθε ηλεκτρόνιο στο άτομο έχει μια μοναδική "διεύθυνση" που καθορίζεται από τέσσερις κβαντικούς αριθμούς. Είναι σαν το ταχυδρομικό κώδικα που καθορίζει ακριβώς πού βρίσκεται!

Ο κύριος κβαντικός αριθμός n (1,2,3...) δείχνει την απόσταση από τον πυρήνα και καθορίζει τη στιβάδα (K, L, M, N...). Όσο μεγαλύτερο το n, τόσο μεγαλύτερη η ενέργεια.

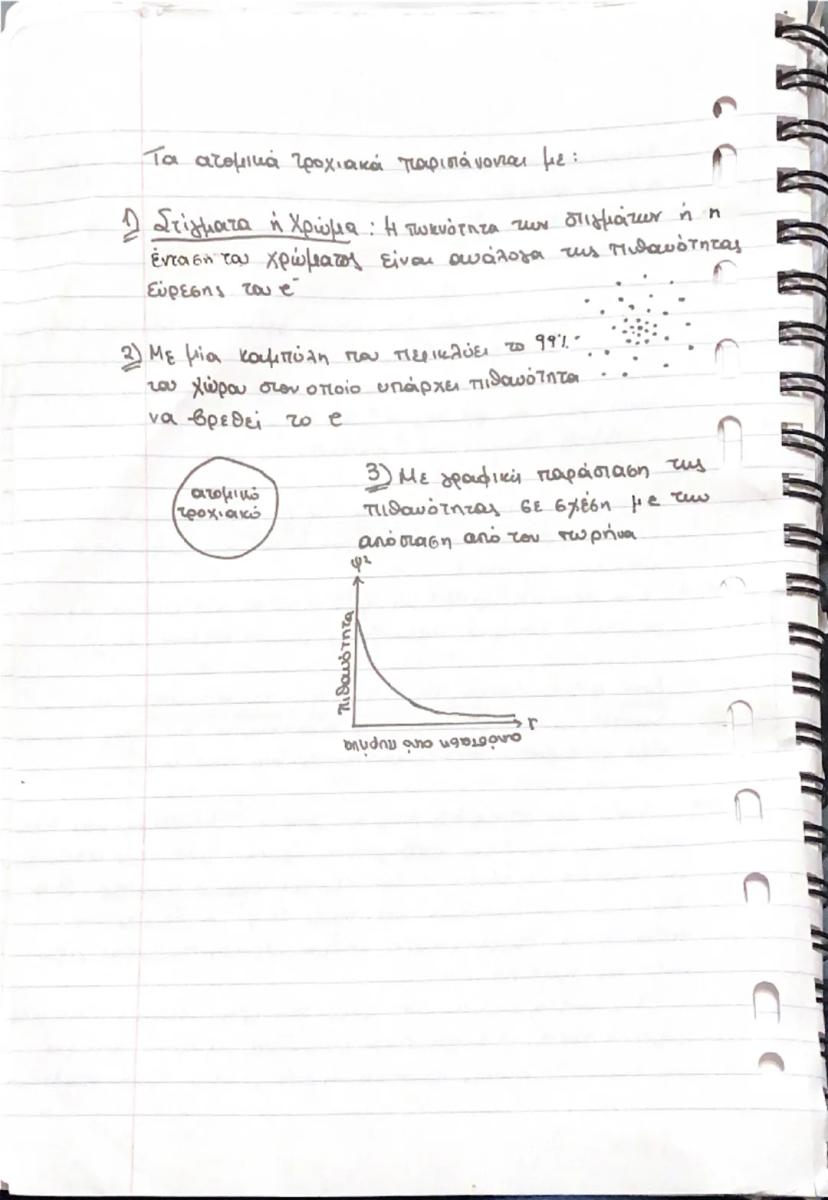
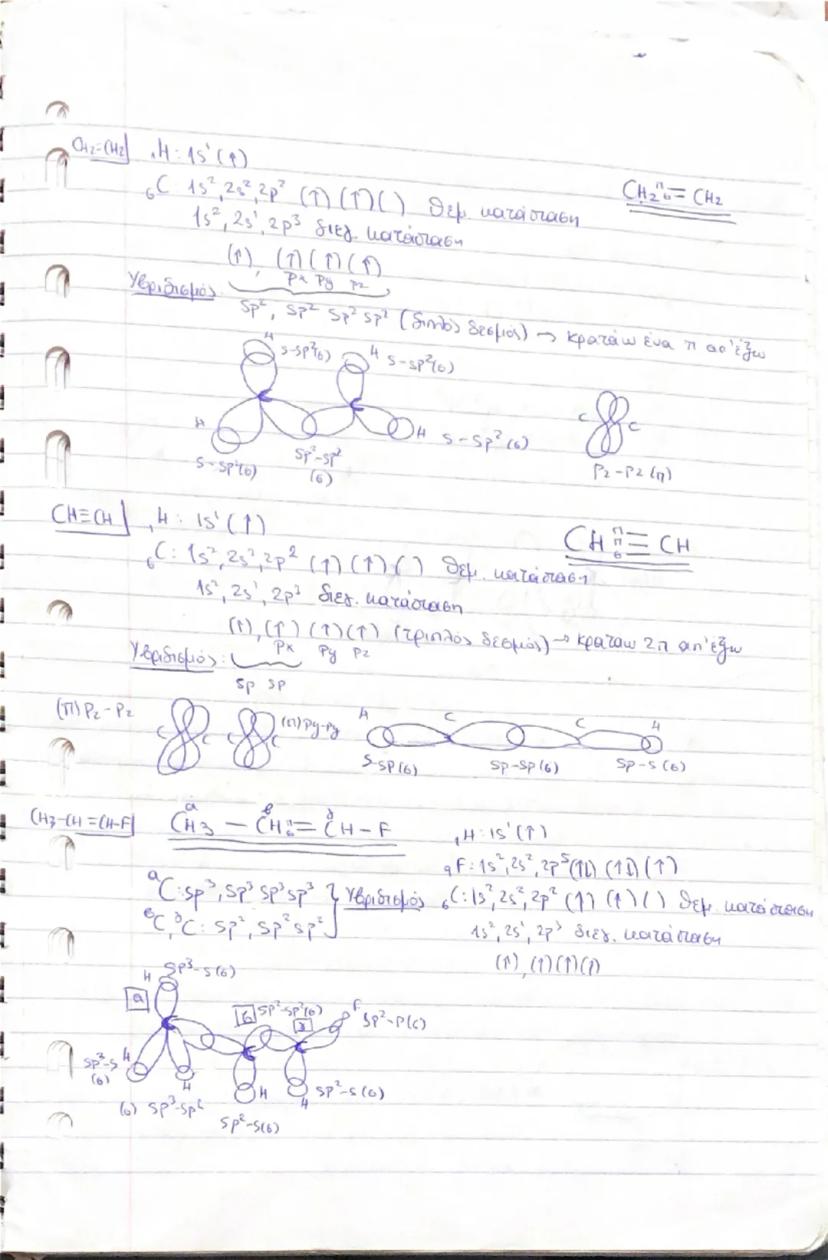
Ο αζιμουθιακός αριθμός l $0,1,2...n-1$ καθορίζει το σχήμα του τροχιακού: l=0→s (σφαιρικό), l=1→p (αλτήρας), l=2→d (πολύπλοκα σχήματα), l=3→f (ακόμα πιο πολύπλοκα). Το ζεύγος (n,l) καθορίζει την υποστιβάδα.

Ο μαγνητικός αριθμός ml $-l...+l$ δείχνει τον προσανατολισμό του τροχιακού. Ο spin ms (±½) δείχνει την "αυτοπεριστροφή" του ηλεκτρονίου.

💡 Θυμήσου: Η τετράδα (n,l,ml,ms) είναι μοναδική για κάθε ηλεκτρόνιο - δεν μπορούν δύο ηλεκτρόνια να έχουν την ίδια!

Τροχιακά s, p, d, f - Σχήματα και Χαρακτηριστικά

Τα s τροχιακά έχουν σφαιρική συμμετρία και η μέγιστη πιθανότητα εύρεσης ηλεκτρονίου είναι πάνω στον πυρήνα. Σε κάθε στιβάδα υπάρχει μόνο ένα s τροχιακό που χωράει 2 ηλεκτρόνια.

Τα p τροχιακά έχουν σχήμα αλτήρα και τρεις προσανατολισμούς (px, py, pz). Έχουν κομβική επιφάνεια - μια περιοχή όπου η πιθανότητα εύρεσης ηλεκτρονίου είναι μηδέν. Συνολικά χωράνε 6 ηλεκτρόνια (3 τροχιακά × 2 ηλεκτρόνια).

Τα d τροχιακά είναι 5 και χωράνε 10 ηλεκτρόνια, ενώ τα f τροχιακά είναι 7 και χωράνε 14 ηλεκτρόνια. Όσο αυξάνεται το l, τόσο πιο περίπλοκα γίνονται τα σχήματα.

Βασική διαφορά: στα s τροχιακά το ηλεκτρόνιο μπορεί να βρεθεί πάνω στον πυρήνα, ενώ στα p η πιθανότητα εκεί είναι μηδέν!

💡 Μνημονικό: s=1 τροχιακό, p=3 τροχιακά, d=5 τροχιακά, f=7 τροχιακά. Πολλαπλάσιασε επί 2 για τα ηλεκτρόνια!

Αρχές Δόμησης Ατόμων - Οι "Κανόνες του Παιχνιδιού"

Για να φτιάξεις τη σωστή ηλεκτρονιακή δομή ενός ατόμου, πρέπει να ακολουθήσεις τρεις βασικούς κανόνες που είναι σαν τους κανόνες ενός παιχνιδιού.

Η απαγορευτική αρχή του Pauli λέει ότι σε κάθε τροχιακό χωράνε μέχρι 2 ηλεκτρόνια με αντίθετο spin. Δεν μπορούν δύο ηλεκτρόνια να έχουν την ίδια τετράδα κβαντικών αριθμών.

Η αρχή ελάχιστης ενέργειας λέει ότι τα ηλεκτρόνια μπαίνουν πρώτα στα τροχιακά με τη μικρότερη ενέργεια. Η σειρά είναι: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d... Χρησιμοποίησε το άθροισμα $n+l$ για να θυμάσαι τη σειρά!

Προσοχή: όταν γράφεις κατιόντα, τα ηλεκτρόνια φεύγουν από την υποστιβάδα που γράφεται τελευταία (οριζόντια σειρά), όχι από αυτή που έχει τη μεγαλύτερη ενέργεια!

💡 Μνημονικός κανόνας: Χρησιμοποίησε το διάγραμμα με τις λοξές γραμμές για να θυμάσαι τη σειρά πλήρωσης!

Κανόνας Hund και Ηλεκτρονιακές Δομές

Ο κανόνας του Hund είναι σαν να μοιράζεις καρέκλες σε μια αίθουσα: πρώτα κάθεται από ένας σε κάθε καρέκλα, μετά μπαίνει ο δεύτερος! Τα ηλεκτρόνια τοποθετούνται με παράλληλα spin σε τροχιακά ίδιας ενέργειας.

Στην πράξη: βάζεις πρώτα από ένα ηλεκτρόνιο (με θετικό spin) σε κάθε p, d ή f τροχιακό, και μετά συμπληρώνεις με το δεύτερο (αρνητικό spin).

Για παράδειγμα: C $Z=6$: 1s², 2s², 2p² → p: ↑ ↑ _ N $Z=7$: 1s², 2s², 2p³ → p: ↑ ↑ ↑ O $Z=8$: 1s², 2s², 2p⁴ → p: ↑↓ ↑ ↑

Για να γράψεις την πλήρη τετράδα κβαντικών αριθμών, ξεκινάς από το τελευταίο ηλεκτρόνιο. Η εξώτερη στιβάδα είναι αυτή με το μεγαλύτερο n και καθορίζει τις χημικές ιδιότητες!

💡 Tip: Ο κανόνας Hund εξηγεί γιατί ο άνθρακας έχει 2 μη ζευγαρωμένα ηλεκτρόνια και μπορεί να σχηματίσει 4 δεσμούς!

Περιοδικός Πίνακας - Η "Χάρτα" των Στοιχείων

Ο περιοδικός πίνακας είναι η πιο έξυπνη εφεύρεση της χημείας! Τα 118 γνωστά στοιχεία είναι τοποθετημένα κατά αύξοντα ατομικό αριθμό, έτσι ώστε στοιχεία με παρόμοιες ιδιότητες να βρίσκονται στην ίδια στήλη.

Ο νόμος της περιοδικότητας λέει ότι οι ιδιότητες των στοιχείων επαναλαμβάνονται περιοδικά. Έχει 18 στήλες (ομάδες) και 7 σειρές (περιόδους). Οι σημαντικότερες ομάδες έχουν ονόματα: αλκάλια (IA), αλκαλικές γαίες (IIA), αλογόνα (VIIA), ευγενή αέρια (VIIIA).

Όλα τα ευγενή αέρια (εκτός το He) έχουν δομή ns²np⁶ - αυτό εξηγεί την σταθερότητά τους. Ο πίνακας χωρίζεται σε τομείς s, p, d, f ανάλογα με το πού μπαίνει το τελευταίο ηλεκτρόνιο.

Τομέας s: ομάδες IA-IIA (δομή ns¹ και ns²), Τομέας p: ομάδες IIIA-VIIIA (δομή ns²np¹⁻⁶), Τομέας d: μεταβατικά στοιχεία $ομάδες IB-IIB$.

💡 Σημαντικό: Το He ανήκει στον τομέα s, παρότι βρίσκεται στην VIIIA ομάδα!

Εύρεση Θέσης Στοιχείου στον Περιοδικό Πίνακα

Για να βρεις τη θέση οποιουδήποτε στοιχείου, χρειάζεσαι μόνο την ηλεκτρονιακή του δομή! Είναι πιο εύκολο απ' ό,τι φαίνεται.

Το μέγιστο n δείχνει τον αριθμό της περιόδου. Για τους τομείς s και p, ο αριθμός ηλεκτρονίων της εξώτερης στιβάδας δίνει τον αριθμό της ομάδας (λατινικό σύστημα).

Για τον τομέα d: το μέγιστο n δίνει την περίοδο, ενώ ο αριθμός της ομάδας = ηλεκτρόνια σε ns + ηλεκτρόνια σε $n-1$d.

Παράδειγμα: Te $Z=52$ → 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ 4s² 4p⁶ 4d¹⁰ 5s² 5p⁴

• Μέγιστο n = 5 → 5η περίοδος
• Εξώτερη στιβάδα: 5s² 5p⁴ (6 ηλεκτρόνια) → VIA ομάδα
• Τομέας p (τελευταίο ηλεκτρόνιο σε 5p)

Ο τομέας f περιλαμβάνει τις λανθανίδες (6η περίοδος) και ακτινίδες (7η περίοδος) - τα στοιχεία του παραρτήματος.

💡 Πρακτικό tip: Μάθε πρώτα να γράφεις δομές με βάση το προηγούμενο ευγενές αέριο - είναι πιο σύντομο!